Dynamic Programming

"Dynamic memory(DP) is a recursion with a cache memory!"

Sitting in DS and Algo lectures, many of us would have thought to cram this topic just before the exam as everything jumps over our heads. But, it seems intimidating because it is poorly taught with some classic problems. Here, are some pieced learnings to reach the solution to some complex problems using Dynamic Programming.

But, to understand DP, it is necessary to understand recursion well, which is not just "function calling itself". Recursion -method of solving a problem where the solution of a problem depends on solutions to smaller instances of the same problem, to learn more about recursion click here. Solving problems via recursion may encounter some overlapping sub-problems that need to be examined repeatedly, thus, to ensure that each sub-problem should be evaluated only once we use Dynamic programming algorithms.

Dynamic Programming simply means to reorganize the recursive approach, in order to reduce the time complexity by storing intermediate results, such that each subproblem is calculated only once.

To understand let's consider the following example-

Problem: Minimum Count

Given an integer N, find and return the count of minimum numbers, the sum of whose squares is equal to N.That is, if N is 4, then we can represent it as: {1^2 + 1^2 + 1^2 + 1^2} and {2^2}. The output will be 1, as 1 is the minimum count of numbers required.

Sample Input :
10
Sample Output :
2

Sample Output Explanation :

10 can be represented as :

1^1 + 1^1 + 1^1 + 1^1 + 1^1 + 1^1 + 1^1 + 1^1 + 1^1 + 1^1

2^2 + 2^2 + 1^2

3^2 + 1^2

As we can see, the output should be 2.

Brute-Force approach: The candid way to solve this problem is to express the given number in all possible representations and find the one with the minimum count. To find possible expressions for any number, the idea is to find the numbers whose square is less than or equals to n. For n = 10, the numbers whose squares are less than or equal to 10 are- 1,2, and 3 ( 4^2 = 16 which is greater than 10). To count the occurrence add one to the result of each recursive call for n = (10-1^2), (10-2^2) & (10-3^2) and then find the minimum of them all.

NOTE: Check if a number is a perfect square, the answer would be 1 in that case ( 9 = 3^2).

#include<cmath>
int minCount(int n){
    if(sqrt(n) == floor(sqrt(n)))   //if a number is a perfect square
    {
        return 1;	  // return 1 (9 = 3^2)
    }
    if(n <= 3)          //1 = 1^2, 2 = 1^2+1^2, 3 = 1^2+1^2+1^2
    {
        return n;
    }
    int a = n;        // The basic illustration would be 1^2+1^2+1^2..
    
    for(int i = 1;i<=n;i++)   // Find the squares <= n
    {
        int x = i*i;
        if(x>n)
        {
            break;      // x has become greater than n.
        }
        else
        {
            a = min(a, 1+ minCount(n-x));  //min of all illustrations.
        }
    }

    return a;
}

Time Complexity

For time complexity analysis consider the recursion tree diagram.

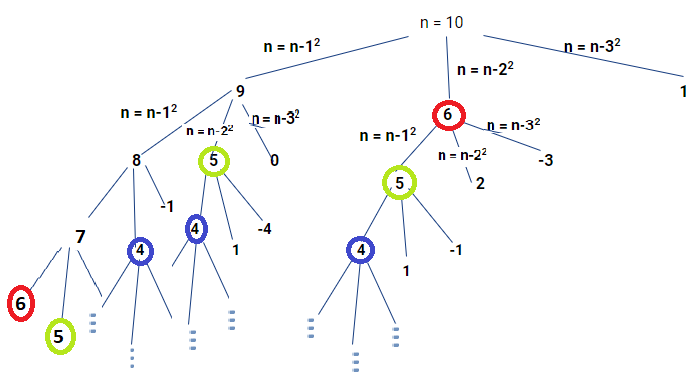
It is evident that the time complexity is exponential, as the algorithm blindly search for every possible combination and then find the minimum. The time complexity for this case is - O(3^n), as for each value of n, 3 recursion calls are made.

Observing the recursion tree diagram carefully, it is discernible that certain recursion calls are redundant, such as n = 4,5,6, etc, the calculation takes place each time the function is called. Thus, to avoid redundant calls we can store the result to some auxiliary space and use it whenever required and the process is termed as Memoization.

Let's code the memoization code for the same problem, For this, declare an output array of size n+1, and initialize it with any number say -1, follow the same algorithm and check if the solution of the current problem already exists, if yes then directly return the value at index n of the output array, else call recursion, find the solution for that problem and then store the result in the respective index of the output array, for the further use.

int helper(int n, int *arr)
{
     if(sqrt(n) == floor(sqrt(n)))   //if a number is a perfect square
    {
        return 1;	            // return 1 (9 = 3^2)
    }
    if(n <= 3)
    {
        return n;
    }
    int ans;
    if(arr[n]!=-1)        //check if already calculated
    {
        ans = arr[n];       
    }
    else            //else find the min and store
    {
        ans = n;
        for(int i = 1;i<=n;i++)   // Find the squares <= n
        {
         int x = i*i;
         if(x>n)
          {
            break;      // x has become greater than n.
          }
         else
          {
           ans = min(ans, 1+ helper(n-x,arr));  // find minimum of all
          }
         }
        arr[n] = ans;    //store the result of n in nth index off arr
    }                    //for future use
    return ans;
}
int minCount(int n){
    int *arr = new int[n+1];    //temporary array.
    for(int i =0;i<=n;i++)    
    {
        arr[i] = -1;            //initialize it with -1
    }

    return helper(n,arr);
}

Time complexity

The Time complexity in memoization apparently decreased due to the elimination of overlapping subproblems. Thus, the total number of unique recursive calls would be approximately 2^n. Thus, the time complexity is O(2^n). But, this is still terrible and needs to be revamped.

Dynamic Programming

Let's think in a reverse manner, for n = 10, the recursion finds the soln. for n = 9, n=6 and n = 1. Similarly, for n = 9, the recursion finds the results for n = 8, n=5, and n = 0, which shows that each problem depends on the solution to their smaller subproblems. Thus, if we have the result for smaller instance we can easily find the answer to our problem. In Dynamic Programming, the aim is to find the instances which are independent and, use them to find the solution for the bigger problems and store them in order to get the desired output. Therefore storing the results iteratively in bottoms-up order can avoid recursion and maintains the results for the smaller instances. Consider the following code for Dynamic programming algorithm:

int minCount(int n){
    if(n <= 3)
    {
        return n;
    }
    dp[0] = 0;            //initialize the independent instance
    dp[1] = 1;
    dp[2] = 2;
    dp[3] = 3;
    for(int i=4;i<=n;i++)        //find sol. for upto n 
    {
        int ans = i;
        for(int j = 1;j<=i/2;j++)
        {
            int k = i - (j*j);
            if(k>=0)
                ans = min(ans,dp[k]+1);
        }
        dp[i] = ans;            //store them for further use.
    }
    int res = dp[n];
    delete[] dp;        // release the extra memory
    return res;                // return answer
}

Time Complexity

The time complexity analysis for this approach involves (n-3)*(sqrt(n-3)) that can be expressed as (n)*(sqrt(n)) .Thus, the time complexity for min count problem using Dynamic programming algorithm is:

         T(n) =  O(n*sqrt(n)) //Better from where we started

Thus, to solve a problem using Dynamic Programming algorithm emphasis on the following:

• Overlapping subproblems.

• Independent instance.

Both of the above factors would help to find an iterative solution for a problem and help to enhance the algorithm.

There are sundry techniques that may yield better results such as Sieve of Eratosthenes algorithm, with time complexity = O(sqrt(n) ). But this blog is completely accentuated on Dynamic Programming, we'll consider this some other day.

I hope this Dissection of Dynamic Programming is fruitful. For complete code visit here

Thank you,

Shreya Sharma

#DynamicProgramming

Github